Pada tutorial sebelumnya, kita melihat langkah-langkah sederhana untuk membaca, menulis, dan memutar file audio. Kami bahkan melihat bagaimana kami dapat mensintesis file audio dari fungsi periodik seperti fungsi kosinus. Dalam tutorial ini, kita akan melihat bagaimana kita dapat melakukan penambahan sinyal, mengalikan sinyal (modulasi), dan menerapkan beberapa fungsi matematika dasar untuk melihat pengaruhnya pada sinyal asli.
Menambahkan Sinyal
Jumlah dari dua sinyal S1(t) dan S2(t) menghasilkan sinyal R(t) yang nilainya setiap saat adalah jumlah dari nilai sinyal yang ditambahkan pada saat itu. Seperti ini:
R(t) =S1(t) + S2(t)
Kami akan membuat ulang jumlah dua sinyal dalam Oktaf dan melihat efeknya secara grafis. Pertama, kita akan membangkitkan dua sinyal dengan frekuensi yang berbeda untuk melihat sinyal yang dihasilkan dari penjumlahan.
Langkah 1:Membuat dua sinyal dengan frekuensi berbeda (file ogg)
>> sig1='cos440.ogg'; %creating the audio file @440 Hz
>> sig2='cos880.ogg'; %creating the audio file @880 Hz
>> fs=44100; %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs); %writing the function cos(w) on the files created
>> audiowrite(sig2,cos(w2),fs);
Di sini kita akan memplot kedua sinyal tersebut.
Plot Sinyal 1 (440 Hz)
>> [y1, fs] = audioread(sig1);
>> plot(y1)
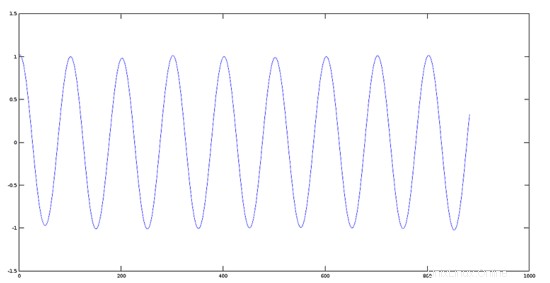
Plot Sinyal 2 (880 Hz)
>> [y2, fs] = audioread(sig2);
>> plot(y2)
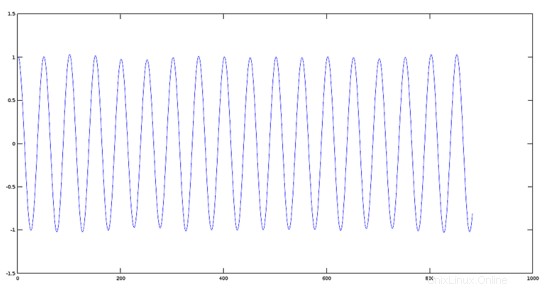
Langkah 2:Menambahkan dua sinyal
Sekarang kita melakukan penjumlahan dari dua sinyal yang dibuat pada langkah sebelumnya.
>> sumres=y1+y2;
>> plot(sumres)
Plot Sinyal yang Dihasilkan
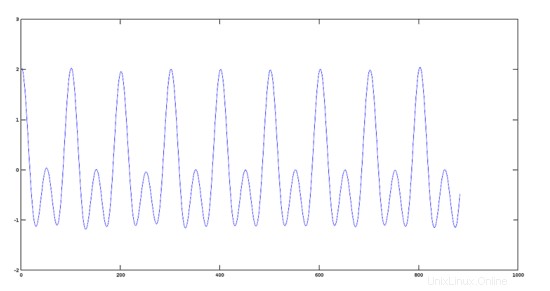
Efek Oktaver
Dalam Octaver, suara yang dihasilkan oleh efek ini menjadi ciri khas karena meniru nada yang dimainkan oleh musisi, baik dalam oktaf yang lebih rendah atau lebih tinggi (sesuai yang telah diprogram), ditambah dengan suara nada aslinya, yaitu muncul dua nada. terdengar identik.
Langkah 3:Menambahkan dua sinyal nyata (contoh dengan dua trek musik)
Untuk tujuan ini, kami akan menggunakan dua lagu Nyanyian Gregorian (pengambilan sampel suara).
Jalur Avemaria
Pertama, akan membaca dan memplot trek Avemaria:
>> [y1,fs]=audioread('avemaria_.ogg');
>> plot(y1)
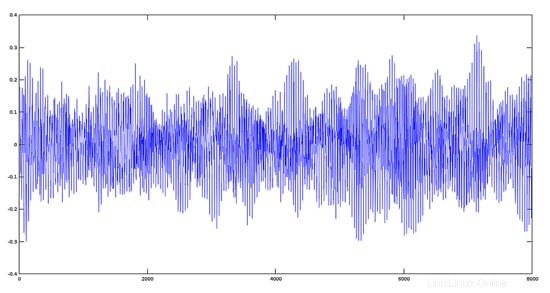
Lagu Nyanyian Rohani
Sekarang, akan membaca dan membuat plot lagu himne
>> [y2,fs]=audioread('hymnus.ogg');
>> plot(y2)
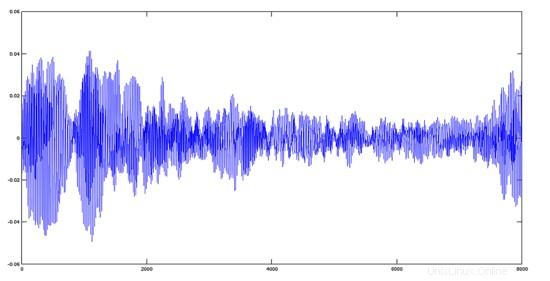
Avemaria + Lagu Nyanyian Rohani
>> y='avehymnus.ogg';
>> audiowrite(y, y1+y2, fs);
>> [y, fs]=audioread('avehymnus.ogg');
>> plot(y)
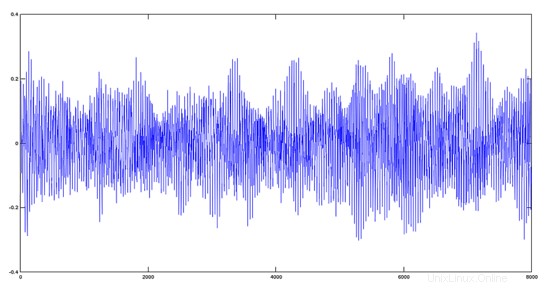
Hasilnya, dari sudut pandang audio, adalah bahwa kedua trek akan terdengar campur aduk.
Produk dari dua Sinyal
Untuk mengalikan dua sinyal, kita harus menggunakan cara yang analog dengan penjumlahan. Mari kita gunakan file yang sama yang dibuat sebelumnya.
>> sig1='cos440.ogg'; %creating the audio file @440 Hz
>> sig2='cos880.ogg'; %creating the audio file @880 Hz
>> product='prod.ogg'; %creating the audio file for product
>> fs=44100; %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs); %writing the function cos(w) on the files created
>> audiowrite(sig2, cos(w2), fs);
>> [y1,fs]=audioread(sig1);
>> [y2,fs]=audioread(sig2);
>> audiowrite(product, y1.*y2, fs); %performing the product
>> [yprod,fs]=audioread(product);
>> plot(yprod); %plotting the product
Catatan:kita harus menggunakan operan '.*' karena produk ini dibuat, dari nilai ke nilai, pada file argumen. Untuk informasi lebih lanjut, silakan merujuk ke manual operasi produk dengan matriks Oktaf.
Plot Sinyal Produk yang Dihasilkan
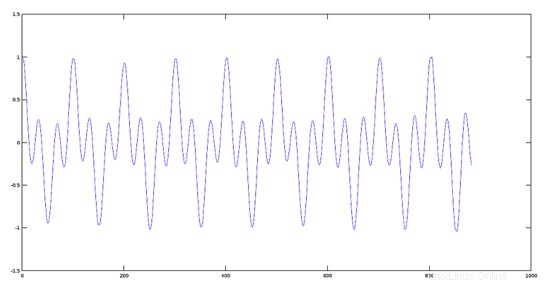
Efek grafis dari perkalian dua sinyal dengan perbedaan frekuensi fundamental yang besar (Prinsip Modulasi)
Langkah 1:
Buat sinyal frekuensi audio dengan frekuensi 220Hz.
>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);
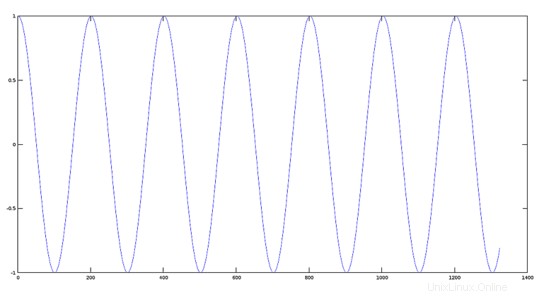
Langkah 2:
Buat sinyal modulasi frekuensi yang lebih tinggi 22000 Hz.
>> y2=cos(100*w);
>> plot(y2);
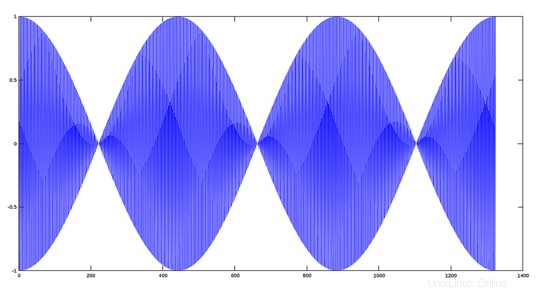
Langkah 3:
Mengalikan dan memplot dua sinyal.
>> plot(y1.*y2);
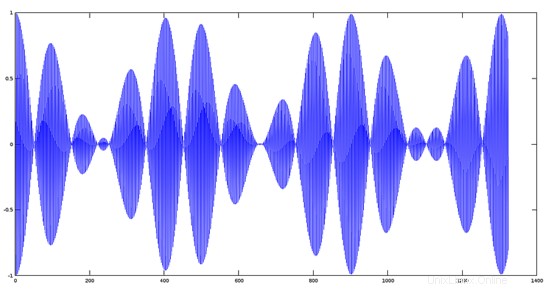
Mengkalikan sinyal dengan skalar
Efek mengalikan fungsi dengan skalar setara dengan memodifikasi ruang lingkupnya dan, dalam beberapa kasus, tanda fase. Diberikan skalar K, produk dari fungsi F(t) dengan skalar didefinisikan sebagai:
R(t) =K*F(t)>> [y,fs]=audioread('cos440.ogg'); %creating the work files
>> res1='coslow.ogg';
>> res2='coshigh.ogg';
>> res3='cosinverted.ogg';
>> K1=0.2; %values of the scalars
>> K2=0.5;
>> K3=-1;
>> audiowrite(res1, K1*y, fs); %product function-scalar
>> audiowrite(res2, K2*y, fs);
>> audiowrite(res3, K3*y, fs); Plot Sinyal Asli
>> plot(y)
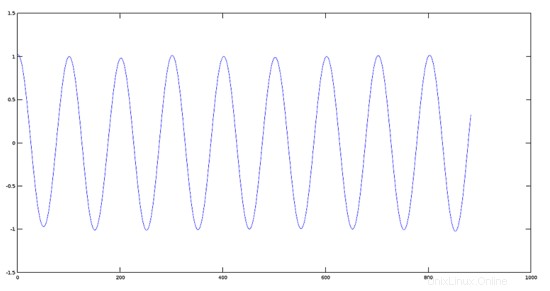
Plot Sinyal berkurang amplitudonya sebesar 0,2
>> plot(res1)
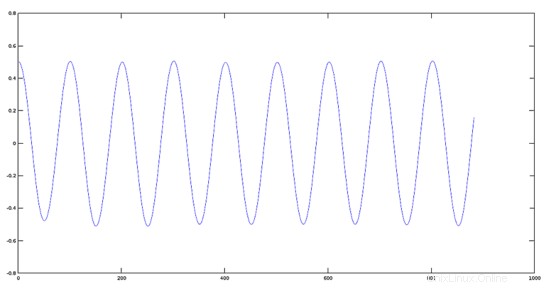
Plot Sinyal berkurang amplitudonya sebesar 0,5
>> plot(res2)

Plot Sinyal dengan fase terbalik
>> plot(res3)
Kesimpulan
Operasi matematika dasar, seperti penjumlahan aljabar, hasilkali, dan perkalian suatu fungsi dengan skalar merupakan tulang punggung dari operasi-operasi lanjutan di antaranya, analisis spektrum, modulasi amplitudo, modulasi sudut, dll. tutorial, kita akan melihat bagaimana membuat operasi tersebut dan efeknya pada sinyal audio.