Dalam tutorial ini, kita akan membahas aljabar vektor dan perhitungan yang sesuai di bawah Scientific Linux. Untuk tujuan kami, saya telah memilih Python sebagai bahasa pemrograman karena kesederhanaan dan kekuatan perhitungannya. Semua distribusi Linux secara default memiliki editor/kompiler Python yang dipanggil melalui jendela terminal. Mari membahas beberapa konsep aljabar vektor.
Catatan:kita hanya akan mengerjakan ruang nyata dua atau tiga dimensi.
Aljabar Vektor
Elemen ruang vektor, dari sudut pandang matematika, dapat direpresentasikan sebagai larik dari sejumlah elemen yang termasuk dalam ruang vektor itu. Lebih khusus, dan dalam pendekatan komputasi numerik, dapat direpresentasikan sebagai daftar bilangan real, yang memiliki tiga karakteristik dasar:
Magnitudo
Ukuran vektor dan dilambangkan dengan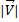 
;ini adalah bagian skalar dari sebuah vektor. Untuk menghitung besarnya vektor kita harus melakukan rumus berikut:
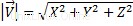
X, Y dan Z adalah koordinat vektor.
Arah
Arah vektor diberikan oleh garis directrix yang memiliki sudut tertentu untuk setiap sumbu sistem koordinat yang disebut sudut direktur.
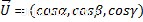
Di mana alfa, beta, dan gamma adalah sudut pengarah vektor dan cosinusnya adalah cosinus pengarah, mereka juga dapat dihitung dengan membagi setiap koordinat vektor dengan besarnya.
Orientasi
Salah satu dari dua kemungkinan orientasi antara arah yang sama.
Jumlah Aljabar Vektor
Untuk membuat jumlah aljabar vektor, kita harus menjumlahkan koordinat homolog dari dua vektor, yang memiliki sifat-sifat yang sama dari jumlah aljabar bilangan real. Seperti berikut:
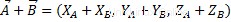Seperti yang kita lihat, hasilnya adalah vektor lain, yang termasuk dalam ruang vektor yang sama.
Produksi vektor dengan skalar
Diberikan vektor dan skalar, vektor hasil kali skalar didefinisikan sebagai produk skalar dari setiap koordinat vektor:
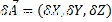
Di mana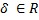 
Vektor Satuan
Aplikasi langsung untuk vektor Produk dengan skalar adalah vektor satuan, a vektor satuan adalah vektor bernorma dengan panjang 1.
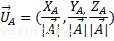
Kombinasi Linier
Ketika kita mencampur operasi sebelumnya, jumlah aljabar dan skala vektor produk, kita memperoleh kombinasi linier, di mana hasilnya juga merupakan vektor yang termasuk dalam ruang vektor yang sama, sebagai adalah:
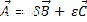
Di mana vektor A adalah kombinasi linier dari vektor B dan C.
Python di Scientific Linux 7.1
Untuk mengimplementasikan aljabar vektor kami memilih Python sebagai bahasa kalkulus. Editor teks yang kami pilih adalah gedit dan hadir secara default dengan distro Scientific Linux 7.1.
Besar dari sebuah vektor
Mari panggil gedit menggunakan terminal atau cukup klik ikon di tab aplikasi:
Pertama kita harus bekerja dengan daftar, sebagai vektor yang mewakili dan harus dideklarasikan sebagai adalah:
V=[2, 2, 1]
Mari kita mendeklarasikan variabel untuk menyimpan besaran dan memberikan nilai, kita menggunakan 0.
modV=0
Sekarang kita menggunakan matematika kelas untuk mengoperasikan akar kuadrat:
import math
Perhitungan besarnya:
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
Seperti yang kita lihat, kita harus menggunakan sub-indeks untuk menunjukkan item dari daftar yang akan kita operasikan, mulai dari 0.
Skrip lengkapnya adalah sebagai berikut:
V=[2, 2, 1]
modV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
print (modV)
Setelah selesai kita harus menyimpan file dengan ekstensi .py dan menemukan jalur file dan membuka jendela terminal di sana dengan klik kanan dan kemudian "buka di jendela terminal". Setelah itu kita harus memanggil juru bahasa python ketikan:
$ python [path]/yourfilename.py
ini akan membuka jendela seperti ini dan memberikan hasil:
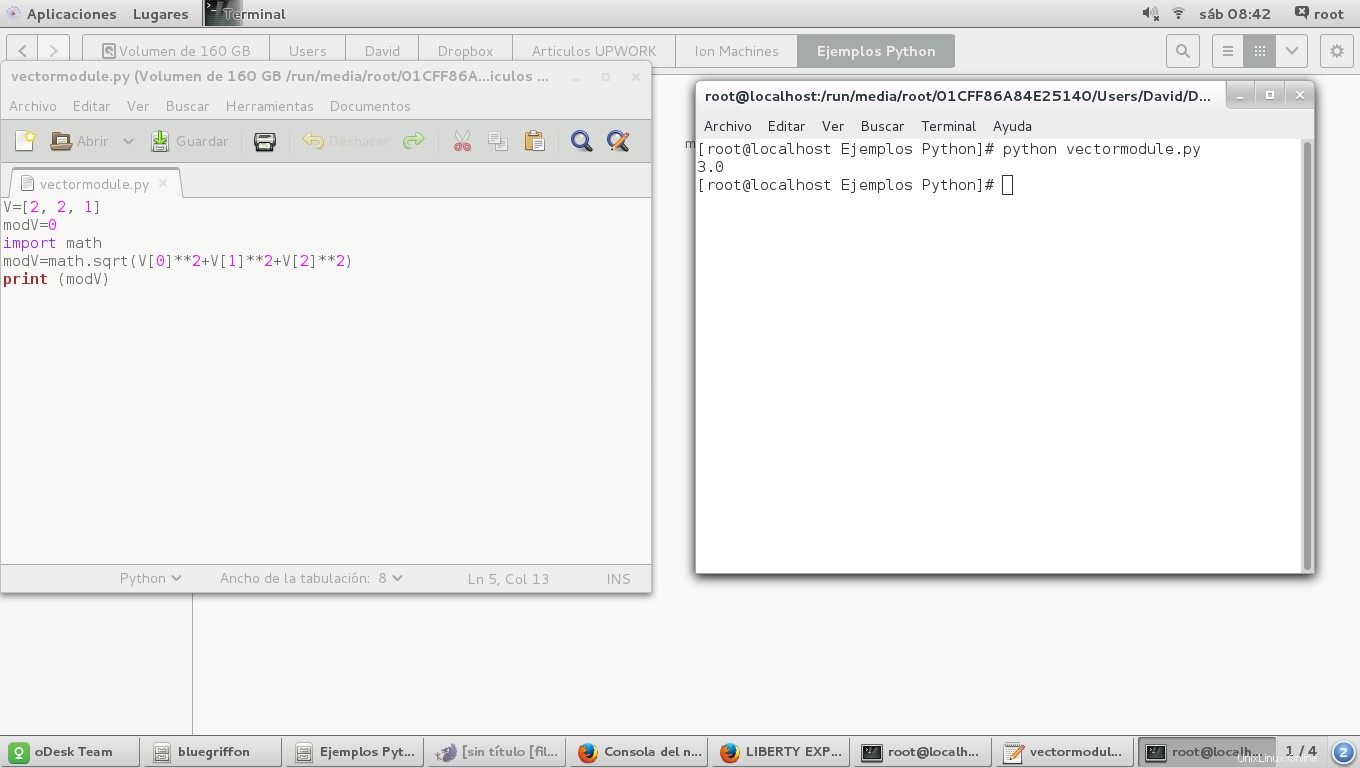
Cara lain untuk melakukannya adalah dengan menggunakan for loop seperti ini:
for x in range (0,3):
modV+=V[x]**2
modV=math.sqrt(modV)
Di sini kita harus menggunakan teknik indentasi karena interpreter python bekerja dengan cara itu.
Arah vektor
Gunakan matematika kelas
V=[2, 1, 2]
modV=0
import math
for x in range (0,3): #loop for calculating the magnitude
modV+=V[x]**2
modV=math.sqrt(modV)
for y in range (0,3): #loop for calculating the director cosines
V[y]=V[y]/modV
print (V)
Hasilnya sebagai berikut:
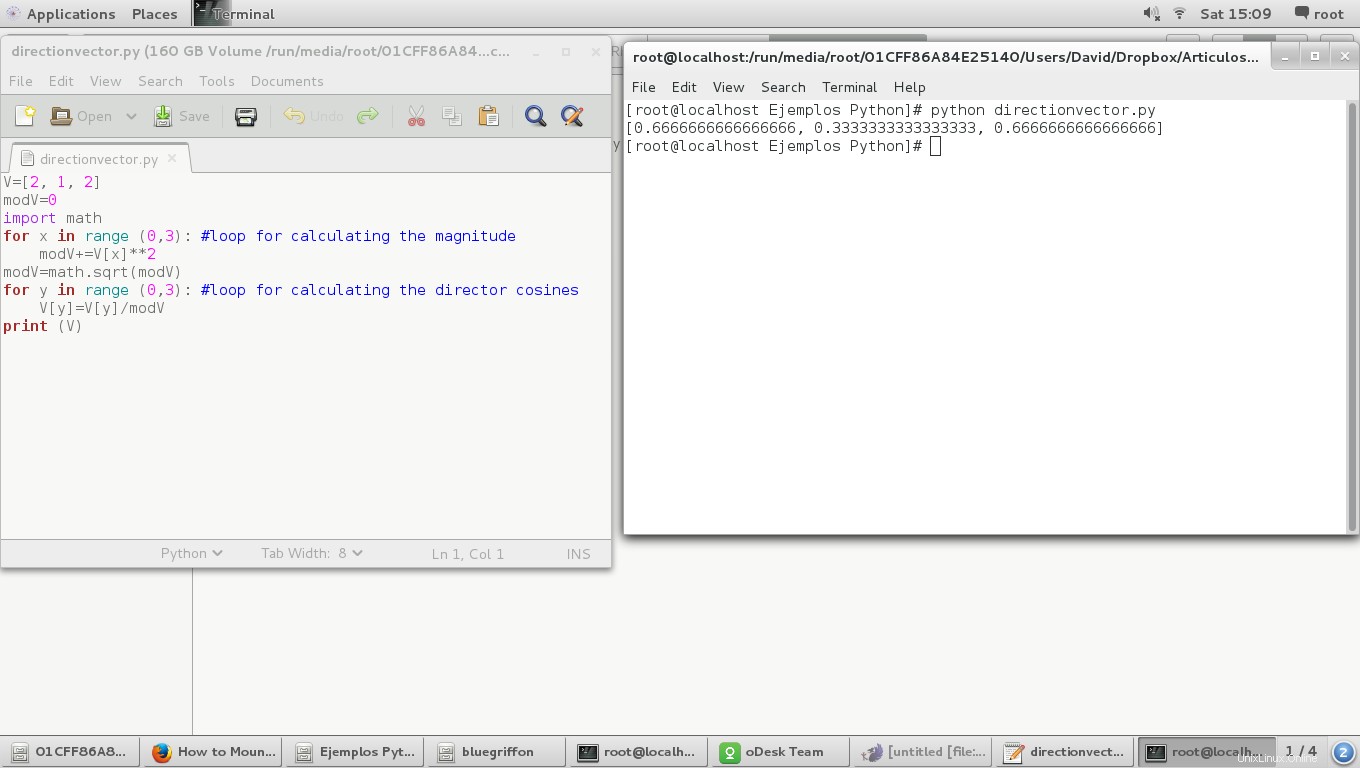
Cara lain adalah menggunakan fungsi trigonometri kelas matematika, cukup seperti ini:
Pertama mari kita hitung sudut sutradara:
V=[2, 1, 2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))
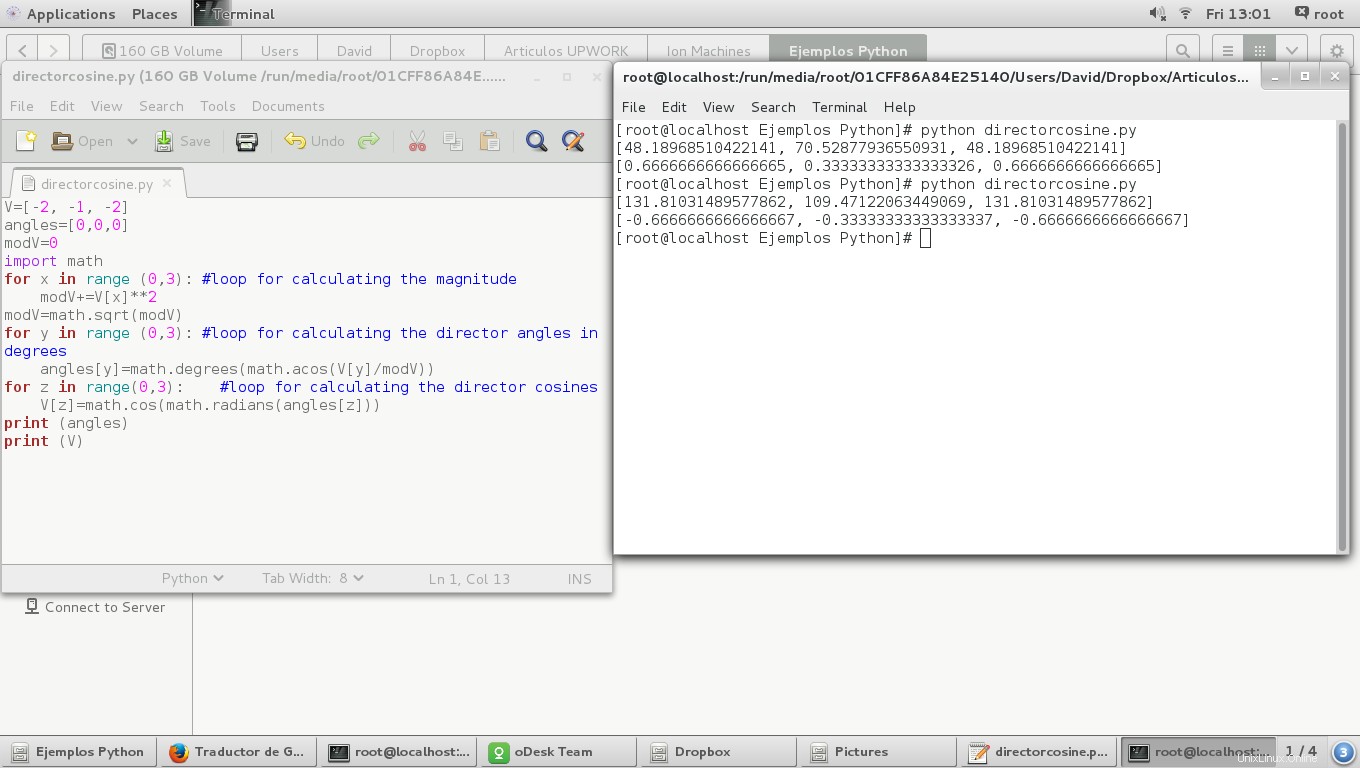
Dan kemudian mari kita hitung cosinus direktur dan mencetaknya
for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
Dan hasilnya:
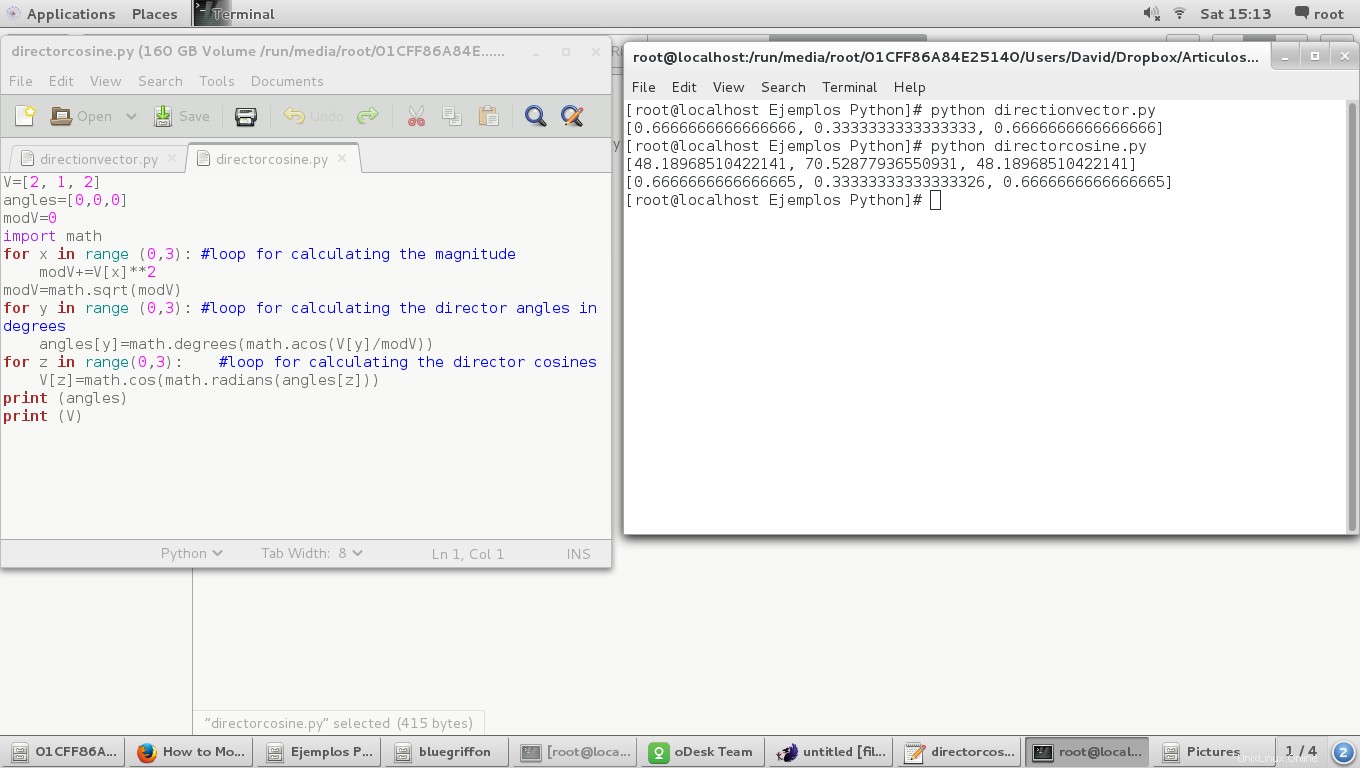
Kita dapat mengamati bahwa cosinus direktur bernilai sama
Orientasi vektor
Jika kita mengubah tanda semua koordinat vektor, kita secara inheren mengubah orientasi vektor, seperti:
V=[-2, -1, -2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
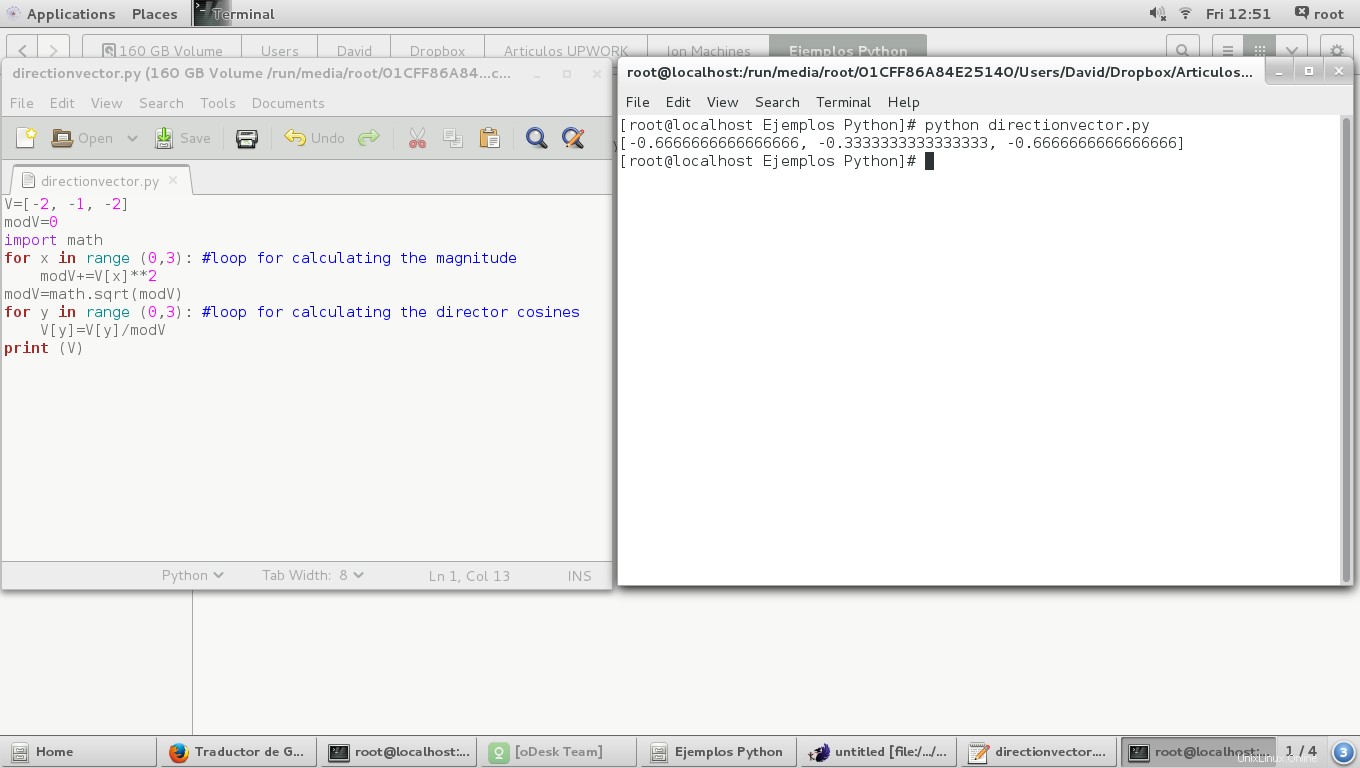
Pada gambar berikutnya kita dapat melihat sudut pengarah yang berbeda 180 derajat dari aslinya
Jumlah Aljabar Vektor
Pertama kita harus mendeklarasikan semua vektor yang terlibat dalam penjumlahan aljabar, seperti:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
di mana kita akan menjumlahkan A plus B dan hasilnya akan disimpan di S
Menambahkan dua vektor (daftar) di Python sama dengan menjalankan loop 'untuk' untuk setiap koordinat vektor yang dihasilkan, jadi kita harus melakukan hal berikut:
for x in range(0,3):
S[x]=A[x]+B[x]
Di sini kita memiliki skrip lengkap untuk penjumlahan vektor aljabar:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
for x in range(0,3): #For loop for adding the homologue coordinate of each vector
S[x]=A[x]+B[x]
print 'S=',A, '+', B, '=', S
Dan hasilnya adalah:
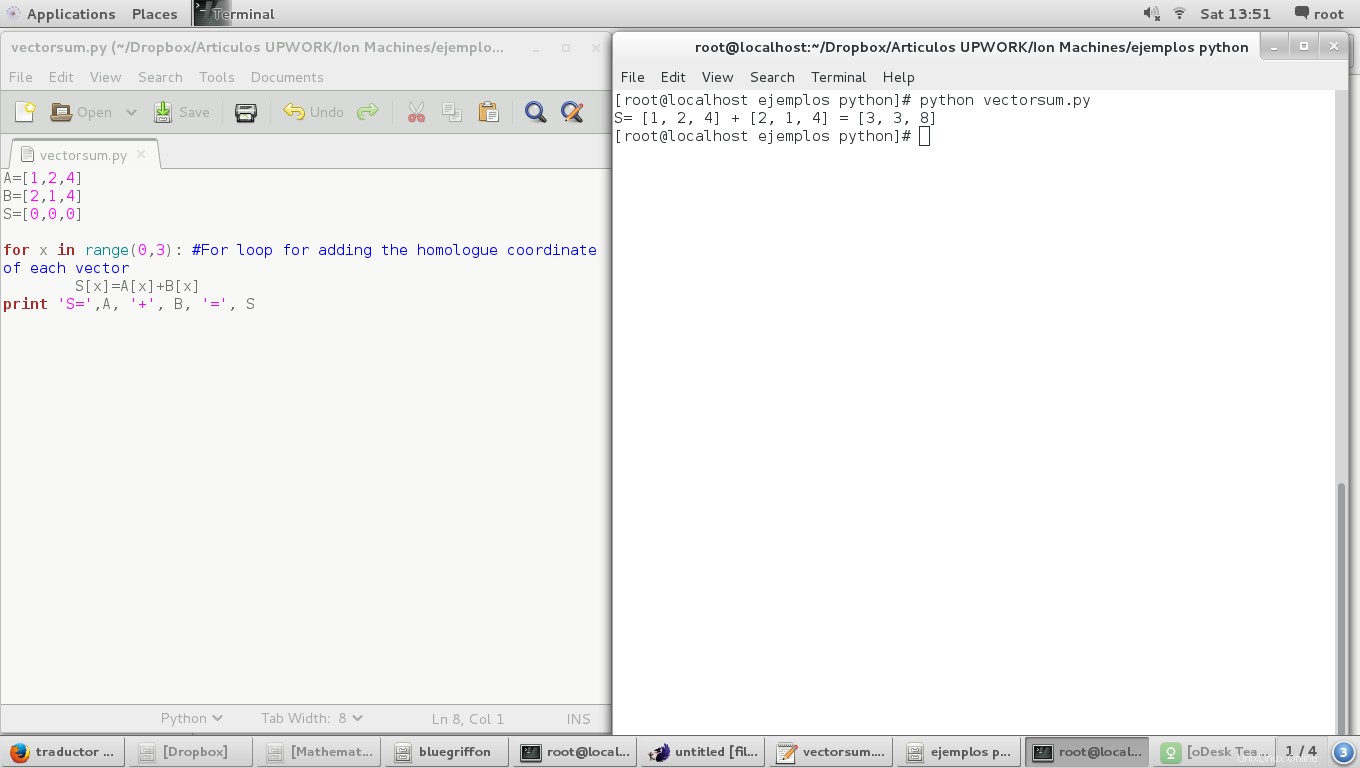
Produk vektor dengan skalar
Diberikan vektor:
A=[1,-2,3]
dan skalar:
scalar=-2
produk vektor dengan skalar didefinisikan sebagai produk skalar dari setiap koordinat vektor:
for x in range(0,3):
R[x]=scalar*A[x]
dan hasilnya adalah:
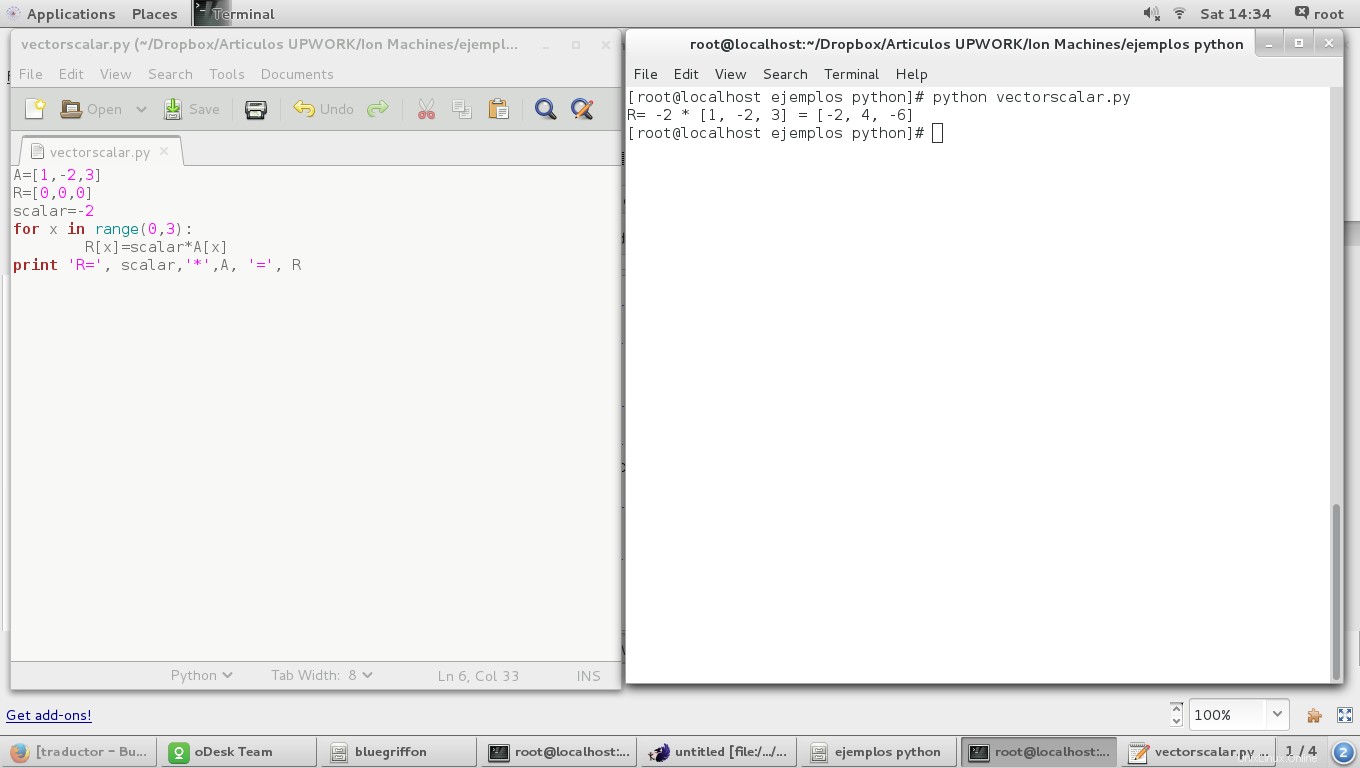
Vektor Satuan
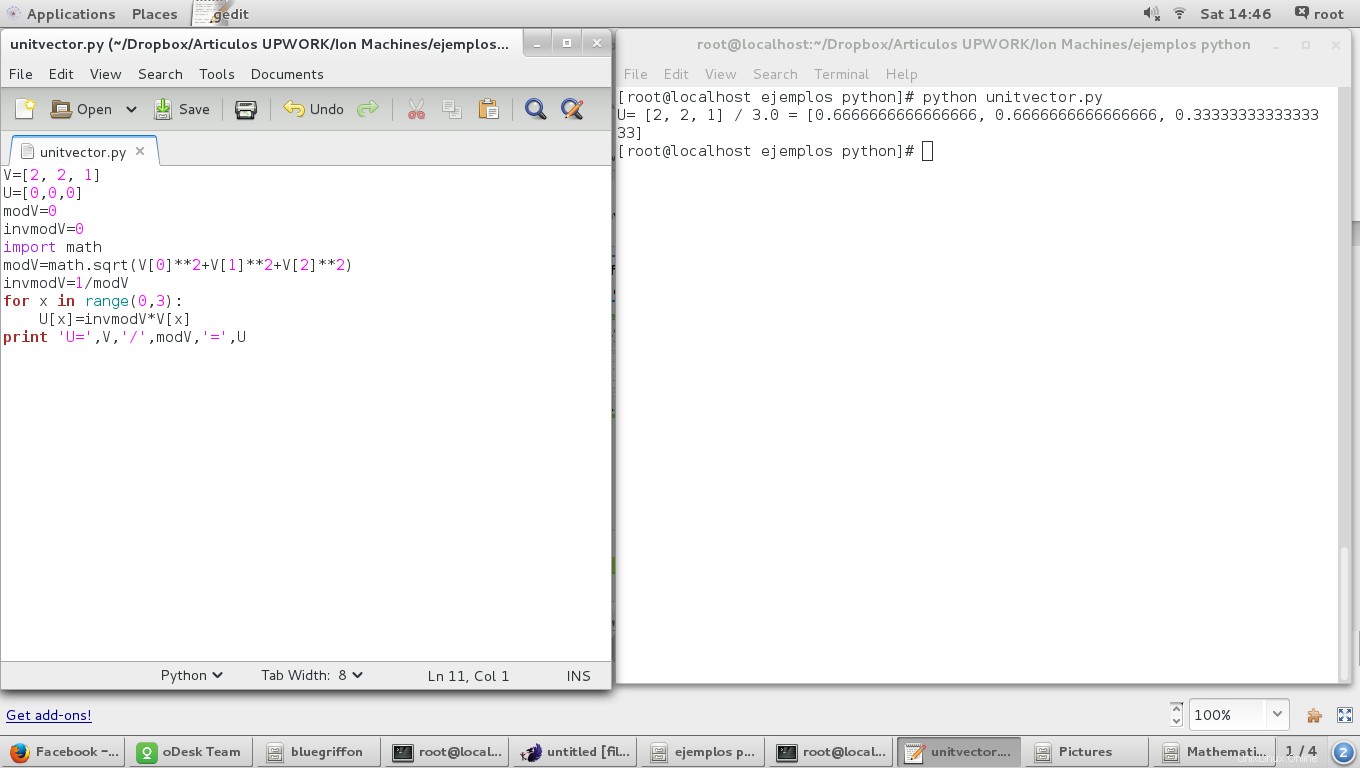
Dengan menggunakan skrip 'Magnitude of a vector' kita memiliki:
V=[2, 2, 1]
U=[0,0,0]
modV=0
invmodV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
invmodV=1/modV
for x in range(0,3):
U[x]=invmodV*V[x]
print 'U=',V,'/',modV,'=',U
dan hasilnya adalah:
Kombinasi Linier
Diberikan tiga vektor , A, B dan C , kita dapat menghitung nilai skalar yang, dikalikan dengan B dan C, masing-masing, menghasilkan vektor A. Dengan kata lain, menempatkan vektor A sebagai kombinasi linier dari vektor B dan C :
A=[7, 9, -8]
B=[1, 3, -2]
C=[-2, 0, 1]
Kombinasi linier mengarah ke sistem persamaan , 3 persamaan dengan 2 variabel ( skalar ) jika tiga vektor r3 , atau 2 persamaan dengan 2 variabel jika mereka adalah dua vektor di R3 , yang dapat diselesaikan dengan menerapkan determinan matriks. Di sini kita harus membuat poin karena tipe data yang ditangani oleh Python. Dalam banyak kasus ketika menghitung skalar yang terlibat dalam kombinasi linier, hasilnya akan memiliki tempat desimal, yang menghasilkan operasi floating point. Tipe data numerik, ditangani oleh Python, adalah:Integer, Real, Long. Jadi, kita harus memasukkan koordinat vektor sebagai tipe data Real, sehingga ini mewakili bilangan real (floating point). Kita harus mengetahui dan memahami beberapa karakteristik tipe data di Python:
- Integer menghabiskan lebih sedikit ruang memori daripada tipe Real.
- Operasi dengan Real lebih lambat daripada Integer.
Di sini kita memiliki vektor yang sama, tetapi dideklarasikan sebagai tipe Real:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
Jadi, dengan ini kita dapat menukar vektor dan dengan demikian selalu memiliki solusi sistem.
Pemeriksaan pertama yang harus kita lakukan adalah apakah ada koplanaritas antara vektor atau tidak, sehingga diketahui ada atau tidaknya adalah kombinasi linier. Untuk itu, kita akan mengimplementasikan matriks determinan:
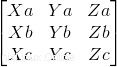
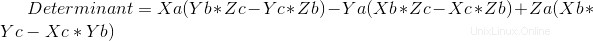
Kode:
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
Jika determinan ini sama dengan nol (0) maka ada ketergantungan linier antara vektor dan kita dapat melanjutkan menghitung skalar. Seperti disebutkan di atas, sistem persamaan memiliki tiga persamaan dengan dua variabel, menghasilkan sistem kompatibel yang ditentukan, di mana kita harus mengambil dua dari tiga persamaan dan menyelesaikan nilai skalar, kemudian periksa dengan persamaan ketiga, tidak diambil sebelumnya, jika sebelumnya nilai skalar menyelesaikannya. Jika mereka tidak menyelesaikan ini, maka tidak ada Kombinasi Linier.
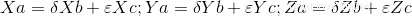
Ini kode lengkapnya:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
if det0==0:
det1=B[0]*C[1]-B[1]*C[0] #First Determinant involving the first and second lines of the equations system
if det1==0:
det2=B[1]*C[2]-B[2]*C[1] #Second Determinant involving the second and third lines of the equations system
if det2==0:
print 'Linear Combination Unexistent'
else:
det3=A[1]*C[2]-A[2]*C[1]
det4=B[1]*A[2]-B[2]*A[1]
sc1=det3/det2
sc2=det4/det2
if sc1*B[0]+sc2*C[0]==A[0]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
det3=A[0]*C[1]-A[1]*C[0]
det4=B[0]*A[1]-B[1]*A[0]
sc1=det3/det1
sc2=det4/det1
if sc1*B[2]+sc2*C[2]==A[2]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
print 'Linear Combination Unexistent'
Dan hasilnya:
[[email protected] ejemplos python]# python lincomb.py
Scalar 1 = 3.0 Scalar 2 = -2.0
[7.0, 9.0, -8.0] = 3.0 * [1.0, 3.0, -2.0] + -2.0 * [-2.0, 0.0, 1.0]
[[email protected] ejemplos python]#
Kesimpulannya, aljabar vektor dasar menghasilkan serangkaian operasi yang melibatkan sistem persamaan linier dan / atau aritmatika sederhana dengan bilangan real. Dalam tutorial lain kita akan melihat bagaimana kita dapat mengembangkan produk dengan vektor, seperti produk titik, produk silang, atau produk campuran.